|
|
|
Back to Orbits Home.
With the assertion that electrons travel in distinct spherical orbits about the nucleus, what mechanism can explain the clustering of atoms into molecules? Two current theories are the Valence Bond Theory and Multiple Bonding Theory. However, I will present an alternative theory based on a simplified intuitive model. We'll start with a pair of hydrogen atoms, that are brought in close proximity to each other. As the atoms get closer, the electrons transition from spherical to circular orbits (In the figure below, the electrons are going into and coming out of the page). The electrons find themselves attracted to the proton of the other hydrogen atom, while they are repelled from each other and tend toward opposite positions. This is illustrated in the following figure.
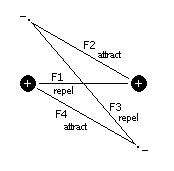
Figure 1 Proton-Electron Force Model
From this model we see that the electrons transition from spherical to circular orbits. In general, the electron-electron distances tend to be maximized, while the proton-electron distances tend to be minimized, all while maintaining their nominal atomic radii. When the forces, F1 through F4 are summed (Fx being proportional to 1/d2), the following plot is obtained:
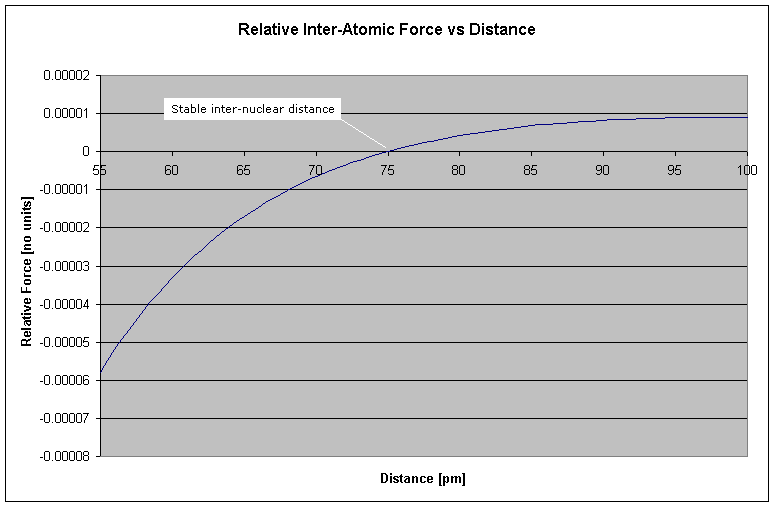
Figure 2 Hydrogen-Hydrogen Bond Length
What this graph demonstrates is that at larger distances the force is attractive (once the orbits have synchronized from spherical to circular orbits), but becomes repulsive beyond a critical distance. This "critical distance" where the net force is zero, becomes the stable inter-nuclear distance - i.e. the bond length. In the case of the paired hydrogen molecule, H2, the bond length is seen from the graph to be 75pm (http://chemviz.ncsa.uiuc.edu/content/doc-resources-bond.html gives the bond length at 74pm).
The simple form of this model, whereby the outer shell forms a "circular" orbit around a packed nucleus of net charge +1, is surprisingly effective for calculating molecular bond lengths for even larger atoms. For example, carbon has 6 protons and 6 electrons forming its charge structure. To construct the model for carbon, we determine its outer shell radius to be 85pm using the Java applet at my atom simulation page. The model assumes that the electrons of the inner shells interact with less influence and thus cancel the positive charges of the protons in the nucleus, leaving us with the simple model of a single electron orbiting a net charge of +1. The graph of two bound carbon atoms is shown below:
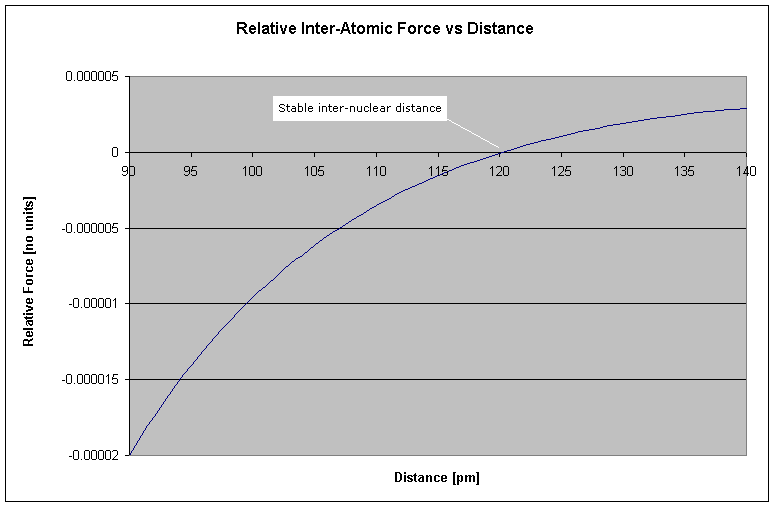
Figure 3 Carbon-Carbon Bond Length
It turns out that the strongest (and consequently, shortest) carbon-carbon bond has a length of 120pm (http://chemviz.ncsa.uiuc.edu/content/doc-resources-bond.html), identical to that shown in the graph.
In summary, the total force = F1 + F2 + F3 + F4, which is proportional to -1/d12 + 1/d22 - 1/d32 + 1/d42. The distances d2, d3 and d4 are geometrically related to d1 and the outer radii of the contributing atoms. It is then a straight forward process to find the zero crossing. However, as one would imagine, such a simple model masks over some complexities, such as, different electron velocities, incomplete transition to a circular orbit, inner shell interactions and multiple atoms bound to a central atom. Fortunately, it is not necessary to address these complexities directly. Since the two nuclei may be approximated as motionless entities, F1 remains proportional to -1/d12. However, F2, F3 and F4 are very much affected by the complexities previously mentioned and we will include an adjustment factor that will subsume these complexities and retain the simple nature of the model. The total force is then proportional to -1/d12 + h/d22 - h/d32 + h/d42, where h = kv and k is determined from measurement. The valence, v, is the strength of the bond and accounts for multiple atoms coupled to a central atom as well other subtle factors that atoms may contribute. The valence is a positive integer value starting at 0, the strongest bond (for example, the CC triple bond is the strongest possible bond and has a valence of 0).
| Table of Valences & Coupling Coefficients |
| Atoms | v | k |
| HH | any | 1.000 |
| CC | any | 0.961 |
| SF | any | 0.978 |
| HB | 1 | 0.958 |
| HC | 1 | 0.955 |
| HN | 1 | 0.953 |
| HO | 1 | 0.949 |
| HF | > 0 | 0.946 |
| HBr | > 0 | 0.942 |
| HI | > 0 | 0.941 |
| HCl | > 0 | 0.938 |
| HS | > 0 | 0.933 |
| HP | > 0 | 0.928 |
| CCl | > 0 | 0.913 |
| NN | > 0 | 0.969 |
| CO | > 0 | 0.971 |
| CN | > 0 | 0.972 |
| SO | > 2 | 0.978 |
| CS | > 2 | 0.977 |
| NO | > 2 | 0.976 |
| OO | > 2 | 0.974 |
The table above lists the minimum valences (i.e. strength) associated with specific atom combinations. No upper bound is given, since kv soon exceeds a point where no zero crossing of the force plot is obtained. Specifically, when kv is less than 0.897, no bond can form.
The model may then be extended to accomodate multiple atoms bound to a central atom as shown in the figure below of the hydrocyanic acid molecule (HCN). There is a natural tendency for the H and N atoms to seek positions at opposite ends of the carbon, since their outer shell electrons are in positions to mutually repel each other. The strength of this repulsion is given an integer valence number where 0 is the strongest and results in a linear molecule (i.e. a bond angle of 180o). The formula for calculating the bond angle is:
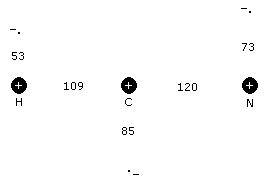
Figure 4 Model of Hydrocyanic Acid
The term, 7v+26(1-e-2.565v), produces the offsets to d1 (0, 31, 40, 47 and 54 @ v = 0, 1, 2, 3 and 4) determined from measurements.
In the case of HCN, the hydrogen-carbon valence is 1, nitrogen-carbon valence is 1 and the hydrogen-nitrogen valence is 0.
These inter-atomic forces can then be simulated, as is shown in my molecule simulation page.