November 2, 1999

Abstract - One fundamental question facing physicists is - has the speed of light been constant throughout time? If the answer is assumed to be yes, then why does it have the value it does (that is, the same distance-to-time ratio)? The following brief paper presents an argument to support the idea that the speed of light is a variable and one that has decreased over time.

First, three premises are asserted, followed by justifications:

• The Law of Conservation of Energy is and always has been true.
• E = mc² is and always has been true (where m is the total mass relative to a non-accelerating reference frame).
• Mass, as an unconserved quantity, may have any positive value.

The first premise asserts that the Law of Conservation of Energy (LCE) is and always has been true. A wealth of evidence supports that this is true today. However, to further defend this assertion, two alternate possibilities could be imagined:

1) energy is decreasing;

2) energy is increasing.

If either of these alternatives is considered, one finds that causality no longer holds. If energy were to come into or out of existence, then macro scale experiments could not be predicted. From one experiment to the next, different results would be obtained due to an increase/decrease of energy in the system¹. From this, we may conclude that a causal universe requires that energy be conserved and that it is a constant within the scope of "universe".

However, this only states that LCE is true today. Perhaps it is possible that at one time in the distant past an "experimenter" could have measured different results. That is, that energy was not conserved. Once it is established that causality requires the conservation of energy, what happens to causality if energy is not conserved? Causality would cease to "be" (i.e. the requirement that the arrow of time is positive ceases to hold, or similarly, events do not require causes). The possibility to travel back in time becomes possible and, as energy is dumped back into the past, it grows without bound² ! Further, if energy is removed from the past, it shrinks until it is zero. If causality had ever ceased to exist (i.e. that LCE was suspended), we would not see the universe of the present day, one where energy is conserved.

The second premise is principally a definition, yet two significant points are evident. First, it defines energy as a state density - that is, m * c * c ³, where mass and the speed of light are the system states. If the system is taken to be the universe, then E_u = m_uc² represents the total energy of the universe. The second point to observe is - what is a property of what? Is energy a property of a massive object or is mass a property of energy? Some consider that energy is a property of massive objects, and, on the surface, this assertion appears justifiable - moving objects are often said to be "energetic". However, since LCE represents the description of an irreducible primary, it is the case that the reverse is true - that mass is a property (or state)⁴ of energy. In fact, it may be considered condensed or stored energy. Mass has no similar conservation law and, in fact, is not conserved in nuclear reactions. An example will help to illustrate. If the scope of an argument is limited to molecules composed of differing atoms, H₂O may be considered an irreducible primary. When it is steam (humidity) we can not build igloos with it, but we are able to measure its presence. When it has cooled (i.e. changed state) it exists substantively. In a closed system, ice would melt into water and water would evaporate into vapor. While the total amount of H₂O would be conserved, ice would not. Therefore, ice is considered a state of H₂O (i.e. H₂O has the property of "form" and takes on the states of ice, water and vapor) and it follows that, the unconserved quantity represents one state of the property of the conserved quantity.

The third premise simply states that, since mass is not a conserved quantity, it may have any value, including one close to zero. There are special conditions, however, for this to occur. Since by LCE the total energy of the universe is a constant (that is, the product of the system states is E_u), an increase in m_u is accompanied by a decrease in c. This premise does not say that mass must have other values, only that it may have other values. However, is there a way to conclude that m_u has varied over time and, if so, in what direction? The first argument arises from the Law of Conservation of Energy. Energy can neither be created nor destroyed, it can only be transformed between states. As mass is one of the states of energy, it may be transformed to another energy-state. Hence, mass is a variable quantity. The second argument is one of causal beginnings and proceeds as follows. Every substantive entity comes into existence by some causative means. Since all massive objects are substantive entities they had to come into existence. Hence, massive objects did not always exist. It is apparent that the first argument describes the premise in more general form, while the second indicates that mass is an increasing variable. A third argument to support this premise uses observations of galactic motion. Galaxies appear to be moving away from each other in an outward direction, suggesting a common region of origin. If this is indeed true, so much mass concentrated in such a small volume could hardly escape the intense gravitational pull⁵. A possible resolution to this problem lies in the idea that the total mass of the universe was much smaller than it is today, resulting in a much smaller gravitational force. Note that this does not express a quantity of matter (either more or fewer particles) - only that the mass was less.

The conclusion drawn from these premises, is that the speed of light is also a variable and, if indeed mass is an increasing quantity, the speed of light is a decreasing one. Hence, there is nothing special about the speed that we measure today - wait a few millions years and it will be different. What experimental evidence is there that the speed of light is decreasing? The accepted value for the speed of light is 299,792,458 m/s and appears to be constant. But the universe is very mature and any change in c would be expected to be quite small, requiring increased precision of measurement to detect it.

Perhaps if we understand what the speed of light represents, a means to detect its change would become evident.

Let us consider a closed system where there are only two massive objects in relativistic motion. The first object will be considered the reference and taken to be at rest. According to the theory of relativity, time dilation and length contraction are observed, by the rest object, to occur to the moving object. There are three distinct entities relevant to the motion of the objects: the objects themselves, electromagnetic fields (light) and space. As the objects will be distant from each other compared to their size, gravitational influence is not a consideration. Of the three entities, only the objects have a substantive quality. Light and space have measurable properties, but are not material. So the question to ask is - is it the object, light or space that is "changing"? Clearly, either object may be considered to be the one "at rest"⁶ and would view the other undergoing time dilation and length contraction. Occupants of either object measure physical laws to be the same. So it can not be the objects actually changing in any substantive way that can be detected in their own frame of reference. Perhaps the light, which we use to make the measurement, is different. Clearly, this is a reasonable possibility. The significant properties of light, as they are generally considered, are magnitude and its orientation, period (a time related property = 1/frequency), phase (also a time related property) and speed of propagation. Every property of light can be affected by motion between the objects except one - the speed of propagation, c. How can this be?⁷ It has already been established that mass is a property of energy and consequently, by similar argument within the relationship of E=mc², the speed of light is also a property of energy. Therefore, c is not a property of light at all. But what is c? It is typically defined as a ratio of distance versus time. But notice that there is a subtle but very important feature (or lack thereof) to any reference of direction - that is, c is a speed, not a velocity. This imposes a very strict limitation on the numerator (distance) as a non-directional quantity.

However, we also asked if space could be changing. Though philosophers have argued about exactly what space is, it is essentially defined by the separation between objects and distance and time separate objects. Hence we may make the statement that space has the properties of distance and temporality. Yet, space has no property of direction - the reference frame, in which measurements are being made, arbitrarily chooses the direction. It becomes apparent that the ratio of the properties of space - distance and temporality - is c, the speed of light. Just as energy is the product of its variable properties, space is the product of its variable properties (distance * 1/time). Therefore, c may be regarded as the complete definition of "space", which is constant⁸, rather than an actual speed of a moving object. For local⁹ phenomena, c could be considered constant, but for non-local phenomena, the change in the value of c must be considered.

To summarize, neither the object (i.e. the physical laws that are measured) nor space is being changed by the velocity between moving objects. These entities remain unchanged, as one would expect¹⁰. We have made a logical progression from the definition of energy as a constant state density of the universe to the speed of light, c, as the fundamental definition of space. Also, it has been shown that, if the initial premises hold, then c is a decreasing variable and, as such, has a derivative. This derivative is an "acceleration" of negative sign (deceleration), and exists throughout space. Returning now to the inquiry: if we understand what the speed of light represents, a means to detect its change would become evident.

Recall that space has no inherent property of direction and that any point in space has a strict limitation to be neutral as to directionality. Also, since the conclusion that a negative acceleration (the first derivative of c) exists throughout space, any point in space "experiences" this negative acceleration, but omnidirectionally. That is, at any point negative acceleration vectors are apparent coming from all directions. All that is needed in order to detect that the speed of light is changing, is to measure this omnidirectional negative acceleration, and the most effective tool for this measurement is mass. Assume that a massive particle (we will also assume it has neutral charge) is placed at some point in space. Since the particle has mass, an inward directed force (F=ma) over its entire surface area becomes evident. As a result, it may be stated that every massive particle is under "spatial pressure". When two such particles are placed in close proximity, it becomes apparent that there is a net reduction in pressure between the particles (force vectors per unit area are in opposition between the particles) resulting in a net attraction. In essence this is the description of gravity. It is comparable to an analogy of two spheres suspended in standard atmospheric pressure, with perpetual vacuum inside and small holes over their entire surface. As the spheres are brought closer together, they tend to attract with greater force.

Is it a reasonable conclusion that gravity is the effect of c's decline? Applying Newton's Law of Gravitation (see Addendum 1) to a massive particle at rest, we could expect to calculate an upper limit to its value¹¹. Using nucleonic density as the particle density and the smallest nucleon mass, that of the electron, as the particle mass, we could expect to arrive at an upper limit. Assuming that the nucleonic density is 2.3e17 kg/m³ and m is 9.11e-31 kg, the acceleration, a, is 1.58e-9m/s². This represents about -0.05 m/s change in c per year¹². As this is not an accurate calculation to the change in c, it serves, nonetheless, as a means to calibrate the theory's claim that the rate of change is very small, as is evident through observation.

Gravity is apparently a constant phenomenon. That is, it appears linear over time. This, however, is a fallacious assumption, since a discontinuity would result (within the context of the presented theory) at the moment c becomes zero (recall that c is a speed, not a velocity, so its value is always a magnitude - a non-negative number). The following proposition states that c is decreasing as the inverse of t (i.e. 1/time) with the result that c and its derivative asymptotically approach zero while mass increases and the mass-acceleration product approaches a constant. If 15 billion years is taken as the age of the universe then c has changed approximately -1.3% over the last 100 million years, representing -0.04 m/s change per year (see Figure 1). If gravity is indeed a phenomenon that is the result of a decline in c, the graviton, aside from its utility as a mathematical convenience, ceases to be relevant.

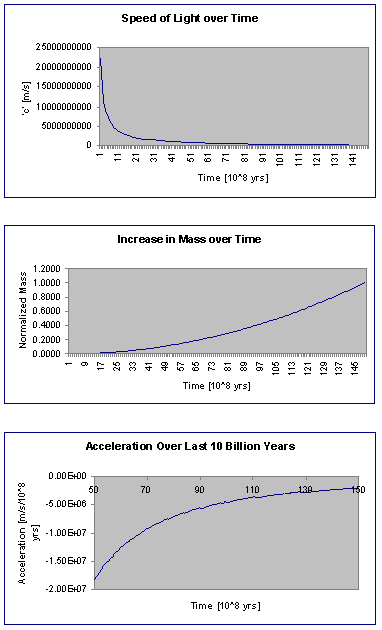
Figure 1 - Speed of Light, Mass and Acceleration Over Time

This paper has set forth the idea that space is separation. As such, space enjoys the properties of distance and temporality, which act as dimensional descriptions in much the same way that a rectangle is described by its properties of length and width. Further, the product of these properties yields what is commonly referred to as the "speed of light". It has been shown that, since time is ever increasing, the speed of light must necessarily decrease. Further, it has been proposed that the first derivative of the speed of light is detectable as gravity.

The goal of this paper has been to discover nature's simplicity. Perhaps, if the fundamental propositions and conclusions described here are indeed sound, additional theories and mathematical models will be developed.