|
|
|
Go to Electron Orbits Home Page
Return to "A Description for Discrete Electron Orbits about the Atomic Nucleus"
Time
Carl Segor
February 5, 2001
Philosophers have argued about the concept of time for many centuries. Does it exist or is it purely a human invention? The universe, as it exists today, is undeniably a causal one. That is, any event must be preceded by another event that causes or at least supports it. For example, for a repetitive waveform, such as a sine wave or triangle wave, to be considered "continuous", it must be uninterrupted for some specified minimum duration. An observer does not expect to see a discontinuity in the waveform or the tenth cycle (perhaps measured by its amplitude) to appear before the fifth. Indeed, it is impossible to argue that we live in a universe that is non-causal for even logic itself requires causal connections between premises and conclusion. And so, in order to place these causal events in chronological sequence, the concept of time - a system of measurement, if you will - was devised to keep track of them. Time, therefore, represents a means to measure the temporal order of events. But is the present system (example: seconds), an accurate way to measure causal events? The answer is no - adequate for most calculations, but clearly not all.
Precision experiments conducted by Albert Michelson and Edward Morley in Cleveland, Ohio during the 1880's showed that the speed of light measured by observers moving at different velocities relative to a source is constant. On the surface, this result does not seem extraordinary. However, when you consider how this differs from our common experience, it is quite extraordinary. Consider for a moment that you are in a space ship cautiously approaching a "stationary" enemy target. As you launch a missile, the enemy target measures the incoming velocity of the missile to be the sum of the space ship's velocity, vs, plus the missile's launch velocity, vm. The velocities are additive, vs + vm. - this is our common experience. However, as the missile was ineffective, you fire a laser cannon. In this circumstance, the enemy measures the speed of the laser to be 'c' (the speed of light), not vs + c! This fabulous experimental result is what exposes the flaw in our simple system of measurement we call time. It must be clearly understood, that we are not stating that causality is violated; in fact, it is quite to the contrary. Causality will be used to show that our "ruler" (i.e. a constant universal time) is indeed flawed.
Again, place yourself on a space ship traveling at velocity, v, toward a large rectangular space station. The station considers itself to be stationary, while you approach with velocity, v. On the other hand, you consider yourself to be stationary, while the station approaches at velocity, v. An experiment is to be conducted, such that, as the ship passes through the station's docking port, it will fire a laser toward the mirrored wall of the dock area (point A in the Figure). Velocity, v, is chosen so that the ship will just be exiting the other docking port when the laser pulse is received (point C in the Figure). The docking authorities on the station see situation A, while you see it as B.
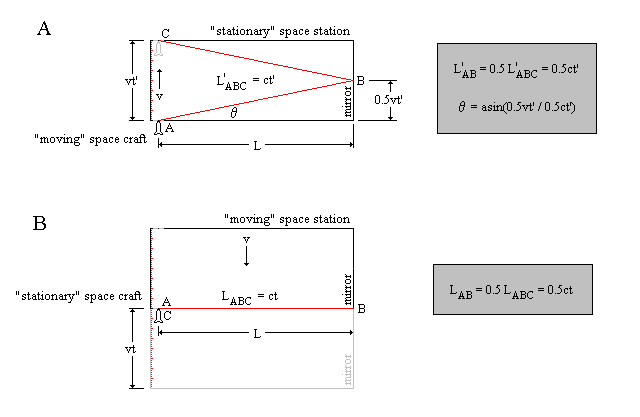
Look closely at the two scenarios. While you observe the path of the laser light to be twice the length of the docking platform (i.e. over and back), the station authorities see a longer path - L'ABC. If the station authorities were to measure the speed of light to be faster (that is, to have an "outward" velocity of 'c' and an "upward" velocity of 'v'), time could be considered the same for both the ship and the station. But this is not the case! Since the station authorities MUST measure 'c' to be the same speed as the ship, something must give, and that thing is our temporal measurement system - time.
Since we know that L is constant, the following relationship holds:
A) L = L'ABcosq
B) L = LAB
Therefore:
L'ABcosq = LAB
0.5ct'cosq = 0.5ct
t' = t / cosq where q = asin(v/c)
At this point you may be saying, "that's all well and good, but time can't be really progressing at different rates, can it?" The answer will be that, since we live in a causal universe - yes. This will be demonstrated, but first we need to understand Doppler shift.
With slight modification, the previous figure can be redrawn to show a stationary reference frame and a moving space ship. Oscillators are present on the ship and at location "A" on the stationary frame. The oscillator is so designed such that, once triggered, it will release a laser pulse directed toward the mirror. In addition, the ship also fires a laser pulse in the aft direction. The received pulse reflected off the mirror will trigger another cycle (i.e. a causal set of events).
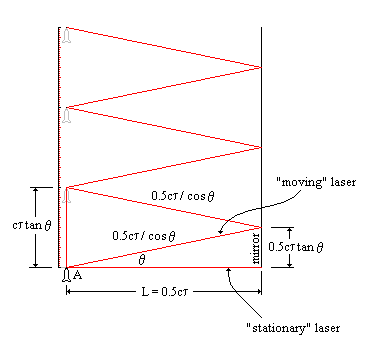
The "stationary" laser pulse travels a path, 2L, equal to ct, where t defines the period of the cycle (1/t is the frequency). The "moving" laser pulse travels the path along the hypotenuse of the triangles and back to point A equal to:
ct' = 0.5ct / cosq + 0.5ct / cosq + ct tanq
t
' = t / cosq + t tanqt
' = t ( 1 / cosq + sinq / cosq )t
' = t [( 1 + sinq ) / cosq ]t
' = t tan(45 + q/2) trigonometric identityThe last equation, t' = t tan(45 + q/2), is the Doppler shift equation expressed in time (i.e. the time for the period of one cycle, where f = 1/t ) for a receding source. For a source that is approaching, the equation is t' = t tan(45 - q/2). So what pulse times does the stationary observer measure from the space ship, if it goes out for three cycles?
1st cycle :t' = 0.5t / cosq + 0.5t / cosq + t tanq = t / cosq + t tanq = t tan(45 + q/2)
2nd cycle :t' = 2 * (0.5t / cosq + 0.5t / cosq + t tanq ) = 2t ( 1 / cosq + tanq ) = 2t tan(45 + q/2)
3rd cycle : t' = 3 * (0.5t / cosq + 0.5t / cosq + t tanq ) = 3t ( 1 / cosq + tanq ) = 3t tan(45 + q/2)
If we draw a line to represent the stationary frame's observations of received laser pulses, for a ship that goes out for 3 cycles and returns, using q = asin(0.5c/c) = 30° , it looks like this:
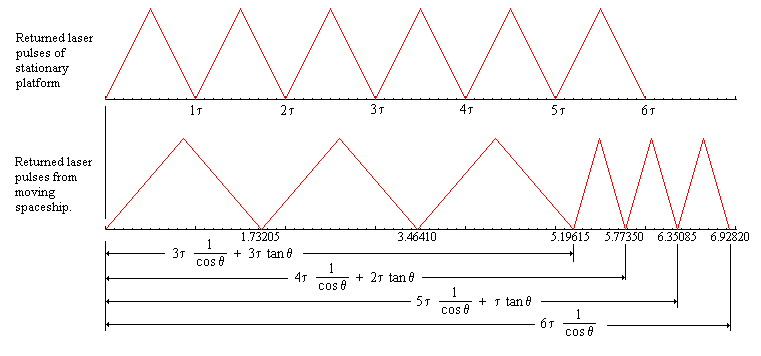
t
' = t tan(45 + q/2) = 1.73205t recedingt
' = t tan(45 - q/2) = 0.57735t approachingIt is apparent from the graph that the final laser pulse from the traveler does not coincide with the stationary observer's final pulse. The difference between the stationary and moving frames is the factor 1/cosq, the time dilation calculated previously. Apart from the acceleration of reversing direction, the moving frame has considered that the laser pulse has traveled the distance 2L for all of the 6 cycles.
We must now concede that in order to maintain a causal sequence of events, the "time" in the moving frame "slows down" by the factor 1/cosq. If instead we chose our oscillator to be an atomic one, we would find the same factor to be evident. Therefore, from atomic interactions through cellular reproduction to aging, the events in the moving frame are stretched out relative to the stationary one.
We can now state that between two moving frames a constant time dilation factor exists. For an accelerating frame an increasing (or decreasing) time dilation factor exists. Thus, when an object is experiencing acceleration, such as a gravitational or electrical field, an increasing time dilation factor is present relative to objects outside of such fields.